Introduction to machine learning

[ I'd be giving a talk to introduce Genifer to some Hong Kong people interested in machine learning.  This is the presentation material. ]

Computer vision

Some of you have told me that you're interested in computer vision, so I'll start with visual perception.

The first thing to know is that the computer vision problem is theoretically already solved.  There is no mystery in machine vision:

When we look at a scene, what we have is a image which is a projection of the scene's objects onto a retina.  The mathematics of such a projection is completely specified by projective geometry, with some changes due to occlusion (blocking of light rays).  The machine vision problem is to compute the inverse of the projection, ie, $f^{-1}$.

Of course you also need a way to represent physical objects in the scene.  There are many data structures designed for that purpose, with Clifford algebra (or geometric algebra) being a more mathematical technique.

So why is the vision problem still unsolved?  I guess it's mainly because researchers try to solve the problem using relatively simple or "clever" mathematical tricks instead of really solving every step along the chain of $f^{-1}$.  To do this would require a large scale project, probably beyond the reach of a single professor with a few grad students.

And if someone takes the trouble to solve vision completely, they might just as well tackle the problem of general intelligence (AGI)!

2 type of machine learning

All of machine learning is a search for hypotheses in the hypothesis space.  The resulting hypothesis may not be necessarily correct, but it is the best given the data and based on some criteria ("scores").

There are 2 major paradigms of machine learning:

1. logic-based learning
   -- hypotheses are logic formulas
   -- search in the space of logic formulas
   -- uses classical AI search techniques
2. statistical learning (including neural networks)
   -- emerged in the 1990s
   -- data points exist in high dimensional space
   -- use geometric structures (planes or surfaces) to cut the space into regions
   -- learning is achieved through parameter learning
   -- includes neural networks, support vector machines, ...

Neural networks

This is a neuron:

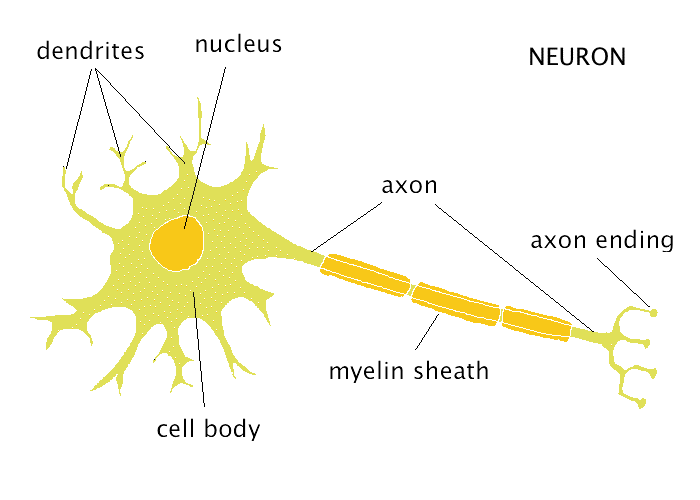
A neuron receives input signals on its dendrites from other neurons.  When the sum of the inputs exceeds a certain threshold, an action potential is fired and propagates along the axon, that reaches other neurons.

Equation of a single neuron

The equation of a neuron is thus:

$$ \sum w_i x_i \ge \theta $$

where the $x_i$'s are inputs, the $w_i$'s are called the weights, $\theta$ is the threshold.

Graphically, each neuron is a hyper-plane that cuts the hyperspace into 2 regions:

Thus imagine multiple neurons chopping up hyperspace into desired regions.

Back-propagation

Back-propagation is a technique invented in the 1970s to train a multi-layer neural network to recognize complex, non-linear patterns.

This is the step function of the inequality $\sum w_i x_i \ge \theta$:

This is replaced by the smooth sigmoid function:

So the equation now becomes:  $\Phi( \sum w_i x_i ) \ge \theta$.

Recall that in calculus, we have the chain rule for differentiation:

$$ D \; f(g(x)) = f ' (g(x)) \cdot g'(x) $$

(The derivative does not exist for the step function because it is not smooth at the threshold point).

Imagine each layer of the neural network as a function $f_i$.  So the chain rule allows us to propagation the error ($\Delta x$) from the lowest layer ($f_1$) to the highest layer ($f_n$):

$$ f_n(f_{n-1}( ... ... f_2(f_1(\Delta x)) ... ) $$

(The formula is just a figurative illustration).  So we can gradually tune the parameters of the neurons in each layer to minimize the error.

Support vector machines

[ See next blog post. ]

Logical / relational learning

This is an example (correct) hypothesis:

$ uncle(X, Y) \leftarrow parent(Z, Y) \wedge brother(Z, X) $

This hypothesis would be too general:

$ uncle(X, Y) \leftarrow $   parent(Z, Y)  $ \wedge brother(Z, X) $

Whereas this one is too specific:

$ uncle(X, Y) \leftarrow parent(Z, Y) \wedge brother(Z, X) \wedge has\underline{ }beard(X) $

Logical inductive learning searches in the space of logic formulas, structured by this general-specific order (also known as subsumption order).

An order (<, Chinese 序) creates a structure called a lattice (Chinese 格).  This is an example of a lattice:


This is another example of a lattice:



Sometimes we use $\top$ to denote the top element (ie, the most general statement, meaning "everything is correct"), and $\bot$ to denote the bottom element (ie, the most specific statement, meaning "everything is false").