「学习」的本质
人脑很多时是通过「一般化 , generalization」来学习的。例如,广东话俗语说:『有须就认老窦』(有胡子便认做父亲,用来取笑过份的一般而论),但可能婴儿就是这样辨认亲人的。
又例如,小时候爷爷教我写中文的「一二三四五」,学到 3 的时候我便自作聪明地说:「我知道了,四字的写法是 4 划!」 虽然是错误的,但表示小孩子的思想方式。
又例如,有些人被女人骗过一次之后,便永远不信女人。
这些都是 generalization 的例子。
相反的方向叫 specialization (特殊化),或 refinement (精细化)。
例如我们从「所有女人都说谎」修正到「有些女人是诚实的」,或者「那个骗我的女人其实也有诚实的一面。」
一般化 和 特殊化 就是逻辑学习的基本运作,没有别的内容了。
此外还有一种机器学习的範畴,是基於在空间中的点的模式识别:
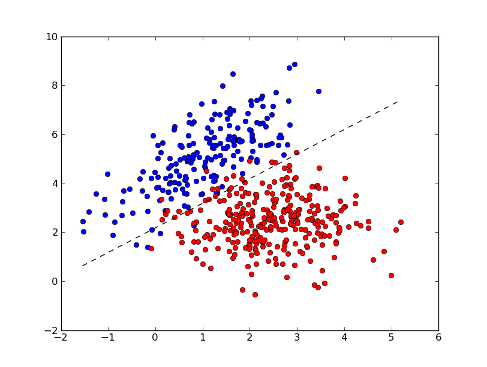
例如我们已经知道有两类东西 (分别标作红色和蓝色),而我们数量化地量度它们的某些特徵,然后在座标空间上点描出来,这时发现红点和蓝点的分布大致可以用一条线分割,於是以后我们只要量度那些特徵,就可以分辨哪些是红组或蓝组的东西,而不需要知道事先知道它们的颜色。
这种「空间中」的统计学习 (statistical learning),其先决条件是知道一些数值上的量度,否则根本没有几何空间可言。 神经网络就是这种 "spatial learning" 的例子。
On the other hand,逻辑学习是不需要几何空间的,它只需要「符号」运作 (symbolic manipulations)。
以下我们专注逻辑学习; 如何统一逻辑学习和空间学习,我觉得是研究的重要课题。
Logic-based learning
例如说,我们观察到「很多读电脑的人都戴眼镜」,但我们是怎样跳到这个「归纳」的结论的?
在逻辑引擎中,已经有的 gound facts (事实资料) 是:
读电脑(小明), 戴眼镜(小明),
读电脑(小娟), 戴眼镜(小娟),
读电脑(小强), 戴眼镜(小强),
读电脑(美玲), 戴眼镜(美玲),
读音乐(小芬),不 戴眼镜(小芬),
男生(小明),男生(小强),
女生(小娟),女生(美玲),女生(小芬),
. . . . . . . 等等。
我们欲求得到的 general rule 是:
读电脑(X) $\rightarrow$ 戴眼镜(X)
其实那算法就是在所有可能的 formula 里面搜寻。
换句话说,由最简单的 formula 开始,我们不断 generate 越来越复杂的 formulas,然后我们逐一试验这些 formulas,看看哪一条最能解释事实。
最简单的 formula 就是一条「空」的命题 (什么也没有,表示一切都是真的)。
然后我们逐步添加一些逻辑项 (terms)。
例如:
$\rightarrow$ 戴眼镜(X)
表示任何人都戴眼镜,但那和事实不符。
又例如:
女生(X) $\rightarrow$ 戴眼镜(X)
「所有女生都戴眼镜」,那也和事实不符。
最后我们试验:
读电脑(X) $\rightarrow$ 戴眼镜(X)
发现其机率很高 (或许有少数例外),於是接受这一假设。
换句话说,这是在「假设空间,hypothesis space」中的搜寻。
这些 search space (搜寻空间) 的结构,形状像「树」那样不断细分下去:
我们由最「一般」的命题 (什么都是真的) 开始搜寻,到越来越特殊的命题,例如「22 岁、五月生日、体重 70 公斤以上、读大学 4 年级、数学不合格、姓张的人 $\rightarrow$ 都戴眼镜」,这过程中必然会出现我们期待的 formula。 这叫 general-to-specific search。
但由於 假设空间里面 有非常多组合 (combinatorial) 的可能性,所以这种学习是很慢的。
似乎唯一的解决之道,就是把所有概念和法则都分类,例如「这是属於物理学的知识」、「这是关於我女朋友的知识」…… 等,而在搜寻时我们只关注那些最可能有关的集合,例如「买礼物给女友时 考虑 class A 的知识」、「物理学考试时 考虑 class B 的知识」 …… 等等。
虽然很难,但必须把这个算法写出来,否则 Genifer 便无望了!
PS: 我在 Genifer 网页里有更详细解释 inductive learning (PDF, in English)。